Le CUBISME
ANNEXE
Retour Le Nombre d'Or, géométrie, Propriétés
La Section d'or
Bien avant que Christo emballe quelques élus, que Buren burine des cailloux qui dépassent et que d'autres fassent les koons il fut un temps où le beau et l'harmonie étaient recherchés. La géométrie permettait de tracer la Divine Proportion et le nombre d'or fascinait les philosophes et les artistes tandis que les Maîtres d'oeuvre et les ésotéristes traçaient des pentagrammes avec respect.
Divine Proportion
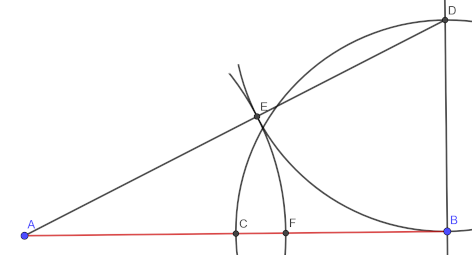
Soit un segment AB que l'on veut partager selon la divine proportion.
- 1. Tracer une perpendiculaire en B
- 2. Déterminer le milieu C de AB
- 3. Au compas reporter C sur la perpendiculaire ce qui donne D
Nous avons donc AB = 2 et BD = 1
- 4. Tracer AD qui vaut racine de 5 soit 2,236 (th. de Pythagore)
- 5. Reporter 1 unité (BD) sur l'hypoténuse à partir de D, ce qui donne E
- 6. Reporter E sur AB , donne F le point cherché
AF vaut racine de 5 - 1
AB sur AF égale AF sur FB égalent le Nombre d'or φ 1,618 (2 divisé par 1,236)
Le Rectangle d'Or
Rectangle d'or
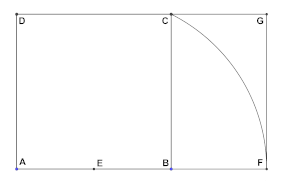
Soit un carré ABCD
- Au compas depuis E milieu de AB reporter C, donne F
- Tracer le rectangle AFGD dans lequel le Grand coté sur le petit égale φ
A Babel, en Egypte, chez les hébreux, les grecs, les romains... cette géométrie était parfaitement connue. Pythagore s'extasiait déjà, l'arithmétique, plus tardive, Aristote transmis par les arabes qui développent l'algèbre, Fibonacci, Brunelleschi, Piero della Francesca, tous en étudiant les propriétés de φ sont amenés à y voir une origine divine dont la nature tire ses proportions et puise sa beauté et son harmonie.
Les architectes soucieux de respecter les proportions de la nature et la volonté divine s'en emparent, les oeuvriers en font un secret d'autant plus jalousement gardé qu'ils ne maîtrisent pas toujours le sujet. Le nombre d'or devient un mythe dont la simple invocation suffit pour magnifier un temple, une cathédrale, une statue ou une peinture.
Disciples de l'occulte, symbolistes, nabis, ésotéristes parent d'un zeste mathématique, donc paraissant rationnel, leur soif de magie et de merveilleux. Mme Blavatsky et sa Théosophie qui débouche aujourd'hui sur le New Age, attrape-tout semeur d'une religiosité prête à se noyer dans les dérives sectaires. Tous font que
φ a de beaux jours devant lui.
Pentagone et Pentagramme
Tracé du Pentacle
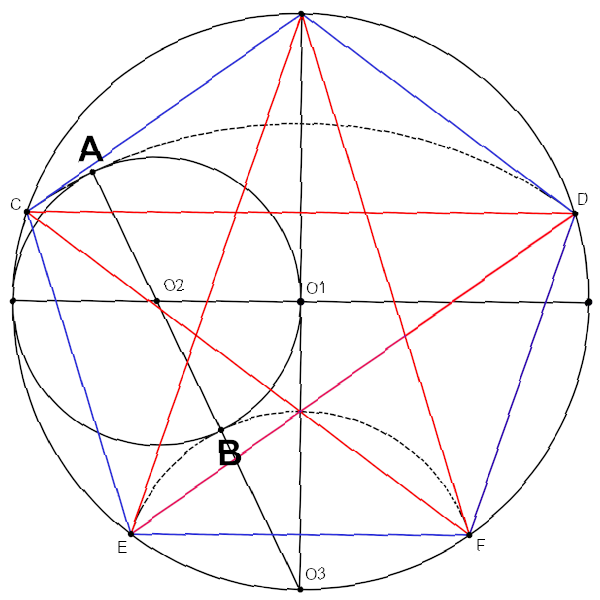
Soit un cercle de centre O1
- Tracer 2 diagonales orthogonales
- Déterminer O2 au milieu du rayon
- Tracer le petit cercle
- Tracer la droite O3 O2
Le reste est lisible, A est équivalent au E du 1er tracé, A et B donnent les 4 points C D E F nécessaires. Le côté du pentagramme (rouge) sur le côté du pentagone (bleu) égale φ.
Fibonacci
Suite de nombres tels que le nombre suivant est la somme des deux qui le précèdent.
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 ...
Le rapport de deux nombres successifs se rapproche de φ d'autant plus que les nombres sont grands.